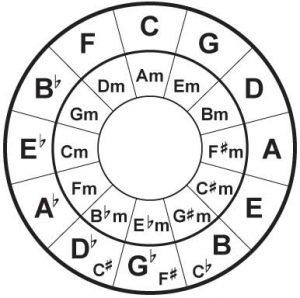
Posiblemente muchos de vosotros hayáis visto este dibujo en alguna ocasión. Se trata del famoso circulo de quintas. Un sistema muy sencillo mediante el cual podemos reconocer el número de alteraciones que posee una composición, las notas de una escala e incluso poder llevar a cabo progresiones de acordes y composiciones de una forma sencilla.
Sistema de representación:
Dibuja un círculo. Divídelo en 12 partes (como si se tratara de un reloj). En la parte superior pon la nota Do. Moviéndonos hacia la derecha, la siguiente nota que vamos a poner es la quinta de Do, o sea, Sol. La siguiente, la quina de Sol, o sea, Re; si seguimos así, aumentando en un intervalo de quinta la nota anterior, nos saldrán estas notas:
Do-Sol-Re-La-Mi-Si-Fa#
Si analizamos cada una de las escalas encontraríamos la siguiente singularidad:
- La escala de Do no tiene sostenidos (0 sostenidos)
- La escala de Sol tiene Fa# (1 sostenido).
- La escala de Re tiene Fa# y Do# (2 sostenidos)
- La escala de La tiene Fa#, Do# y Sol# (3 sostenidos)
- La escala de Mi tiene Fa#, Do#, Sol# y Re# (4 Sostenidos)
- La escala de Si tiene Fa#, Do#, Sol#, Re# y La# (5 Sostenidos)
- La escala de Fa# tiene Fa#, Do#, Sol#, Re#, La# y Fa (ya que Mi# no existe, solo de forma teórica) (en teoría 6 sostenidos).
Si analizamos, por tanto, la construcción de la escala comprobaremos que siempre se cumple la siguiente premisa. SOL tiene una alteración que es justo la que se encuentra a 1 SEMITONO menos que la nota que le da el nombre a su escala.
Re guarda 2 Alteraciones: La que se 1 encuentra a un semitono por detrás de de RE (DO#) y la que guardaba de la escala anterior (escala de SOL: FA#)
Y así sucesivamente…
¿Y cual sería el método para las escalas si contamos las notas bemoles? (hacia la izquierda)
La regla a aplicar ahora será muy similar al caso anterior: la escala de la nota donde nos paremos tendrá los mismos bemoles que la escala de la nota anterior más el bemol que le sigue en el círculo.
Tendremos este resultado:
- La escala de Do no tiene bemoles (0 bemoles)
- La escala de Fa tiene Sib (1 bemol)
- La escala de Sib tiene Sib y Mib (2 bemoles)
- La escala de Mib tiene Sib, Mib y Lab (3 bemoles)
- La escala de Lab tiene Sib, Mib, Lab y Reb (4 bemoles)
- La escala de Reb tiene Sib, Mib, Lab, Reb, y Solb (5 bemoles)
- La escala de Solb (enarmónico de Fa#) tendría Sib, Mib, Lab, Reb, Solb y Si (ponemos Si, ya que el siguiente bemol que le correspondería sería Dob que como sabemos sólo existe desde el punto de vista teórico) (6 bemoles teóricamente)